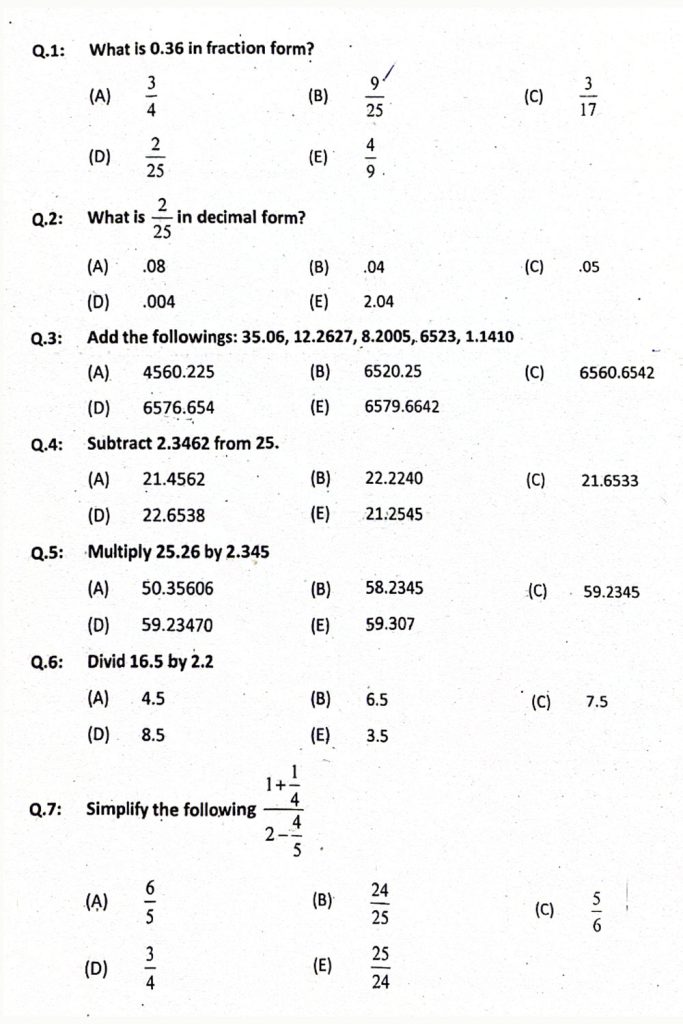
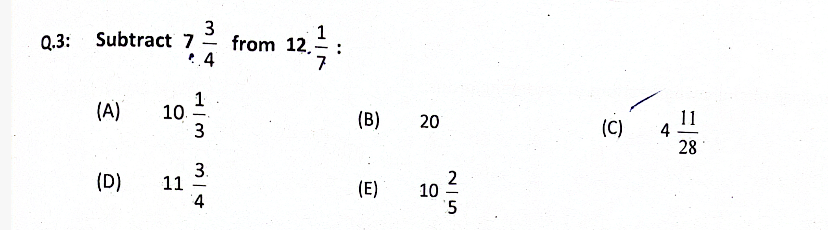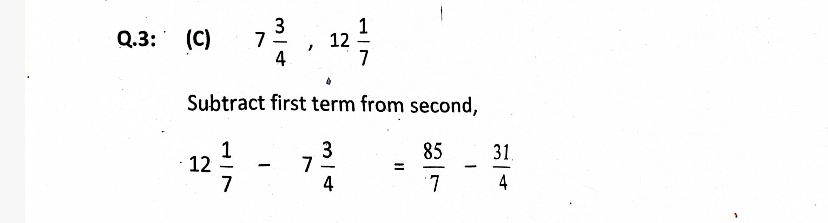Introduction to Fraction and Decimal
Note: Before solving MCQs students much go through the following concepts.
Quantitative Reasoning (Fractions and Decimals)
When a whole is divided into “n” equal parts, each part is called one nth of the whole, written 1/n.
For example, if a cake is cut (divided) into 4 equal slices, each slice is one fourth (1/4) of the cake;
- A day is divided into 24 equal hours,
- So an hour is one twenty-fourth (1/24) of a day;
- And an inch is one twelfth of a foot. (1/12)
Fraction:
Numbers such as 5/4, 8/8 and 3/12 in which one integer is written over a second integer, are called fractions. The center line is called the fraction bar. The number above the bar is called numerator, and the number below the bar is called the denominator.
- A fraction, such as 3/20 in which the numerator is less than the denominator, is called proper fraction. Its value is less than 1.
- A fraction, such as 20/12 in which the numerator is more than the denominator, is called an improper fraction. Its value is greater than 1.
- A fraction, such as 4/4 in which the numerator and denominator are the same, is also improper, but it is equal to 1.
It is useful to think of the fraction bar as a symbol for division. If two fruit cakes are divided equally among seven people, each person gets 2/7 of a cake. If you actually divide 2 by 7, you get that 2/7 = 0.285
Decimals:
1. A decimal, which is a number with a decimal point(.), is actually a fraction, the denominator of which is understood to be 10 or some power of 10.
- The number of digits, or places, after a decimal point determines which power of 10 the denominator is. If there is one digit, the denominator is understood to be 10; if there are two digits, the denominator is understood to be 100, etc.
Example: 0.7 = 7/10; 0.37 = 37/100
- Every fraction, proper or improper, can be expressed in decimal from (or as a whole number) by dividing the numerator by the denominator.
5/9 = 0.55 3/4 = 0.75
2. The addition of zeros after a decimal point does not change the value of the decimal. The zeros may be removed without changing the value of the decimal.
Example: .3 = .30 = .300, and vice versa: .300 = .30 = .3.
3. Since a decimal point is understood to exist after any whole number, the addition of any number of zeros after such a decimal point does not change the value of the number.
Example: 8 = 8.0 = 8.00 = 8.000.
Comparing Fractions:
In this type of question, you may have to compare two or more fractions and determine which is larger, or smaller.
There are two methods of comparing fractions:
- Convert them to decimals (by dividing),
- Cross-multiply.
For example, to compare 1/3 and 3/8 we have two choices.
Write 1/3 = 0.33….. And 3/8 = 0.375 since .375 > .333, then 3/8 > 1/3.
Cross-multiply; 1/3 X 3/8. Since 3 × 3 > 8 ×1, then 3/8 > 1/3.
8 < 9 3/8 > 1/3 Ans.
Tip:
If the difference between numerator and denominator of one fraction is the same as the difference between the numerator and denominator of the other fraction, then the fraction with greater numerator is greater.
Example:
In case of 2-3 6-7 Since 6 is greater than 2 the difference between 2 and 3 is “1” same as difference between 6 and 7. 6 50 is greater fraction. 7